2016.05.17. - Magyar kutatók korszakalkotó új égi mechanikai eredménye
Newton és Lagrange kétszáz esztendőnél is régebbi eredményei után először sikerült explicit, egzakt analitikus megoldást találni az égi mechanikai n-test probléma egyik alosztályára az ELTE két kutatójának.
Az n darab, csak gravitációsan kölcsönható, pontszerűnek tekintett test mozgását vizsgáló n-test probléma a csillagászat és űrkutatás központi jelentőségű kérdése, hiszen döntő szerepe van az égitestek és a mesterséges űreszközök pályájának meghatározásában. Bár a kéttest-probléma általános megoldását már Newton megadta (ennek tulajdonságait összegzik a bolygómozgás jól ismert Kepler-féle törvényei), 2-nél nagyobb n értékek esetére általános megoldás nem létezik. A háromtest-probléma megoldásainak egy alosztályát, az ún. centrális konfigurációkat Euler és Lagrange határozták meg analitikusan a 18. században. Ezek közül a Lagrange-féle megoldásoknak léteznek kézenfekvő általánosításai több test esetére is: 4 test esetében ezek tetraéder alakú konfigurációkat jelentenek.
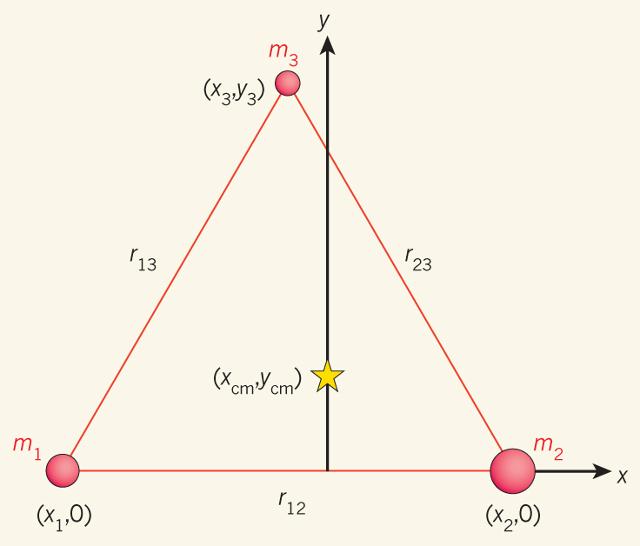
Az m1, m2, m3 tömegű testek mozgása - ha csupán a kölcsönös gravitációs vonzóerőket vesszük figyelembe - analitikusan (egyszerű matematikai függvényekkel) csak akkor írható le, ha a három test egy egyenlő oldalú háromszöget alkot. Kimutatható, hogy a mozgás során a konfiguráció jellege megmarad, a testek mindig egy, az xy síkban elhelyezkedő egyenlő oldalú háromszög csúcspontjaiban lesznek, annak az oldalhossza azonban csökkenhet vagy növekedhet. A sárga csillag a rendszer tömegközéppontját jelöli. A kölcsönös távolságokat a tömegekkel indexelt r betűk, a tömegek és a tömegközéppont koordinátáit pedig (x,y) párok jelzik.
[Nature]
További egzakt, explicit analitikus megoldások azonban nem születtek az n-test problémára, egészen az ELTE TTK FFI két kutatója, Érdi Bálint emeritus professzor és Czirják Zalán PhD hallgató új eredményéig, amelyekben a síkbeli, szimmetrikus négytest-probléma centrális konfigurációira adnak teljes, egzakt és explicit analitikus megoldást.
A síkbeli, szimmetrikus négytest-probléma deltoid alakú konfigurációkat jelent, ahol a deltoid avagy sárkány-alakzat "szárnyait" alkotó két test tömege azonos. Centrális konfigurációnak pedig az olyan elrendezéseket nevezzük, ahol a testekre ható erő a rendszer tömegközéppontjába mutat.
Az áttörést két igen eredeti ötlet tette lehetővé. Egyrészt a hagyományos, például Descartes-féle vagy polárkoordináták alkalmazása helyett az alábbi ábrán α-val és β-val jelölt szögekkel paraméterezik a vizsgált konfigurációkat. Másrészt, eltérően a szokásos megközelítési módtól, ahol a testek tömegét rögzítve keresik a mozgás során alakjukat megőrző centrális konfigurációkat, az ELTE kutatói az inverz problémát oldották meg: adott konfigurációhoz keresték meg azokat a tömegarányokat, amelyek mellett a centrális konfiguráció fennmarad. A számítás így is igen összetett, az eredményeket teljes részletességgel ismertető kézirat terjedelme 57 oldal, az eredményeket a szakmai nyilvánosság előtt bemutató, "tömörített" publikációé pedig 38 oldal.
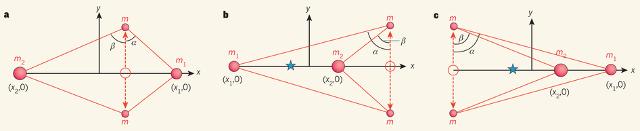
Érdi Bálint és Czirják Zalán a négytest-probléma egyik alosztályára adtak új megoldást, amely a háromtest-probléma azon speciális esetéből származtatható, amikor kezdetben a három test mindegyike az x tengely mentén helyezkedik el. A fenti ábrán mindhárom esetben az m1 és m2 tömegek az x tengelyen maradnak, a harmadik tömeg (eredeti pozícióját üres kör jelöli) pedig két egyforma, m tömegű részre oszlik, és y irányban szimmetrikusan, egyenlő távolságra kerül az x tengelytől (szaggatott nyilak). A tömegközéppont koordinátái (0,0), a tömegeket összekötve pedig konvex (a), illetve konkáv (b és c) poligonokat kapunk. A b) és c) ábrán a kék csillag jelöli az m2 tömeg elhagyásával kapott rendszer tömegközéppontját, a két esetet az különbözteti meg, hogy a kék tömegközéppont a poligonon belülre vagy azon kívülre esik. Az m1 és m2 tömegek helyzetét derékszögű koordináták, a másik kettőét pedig az α és a β szögek határozzák meg.
[Nature]
Az eredményeket részletező szakcikk a Celestial Mechanics and Dynamical Astronomy c. folyóiratban jelent meg, a világ vezető természettudományos folyóiratának számító Nature 2016. május 12-i számában pedig meghívott szerkesztőségi cikkben méltatja Érdi Bálint és Czirják Zalán eredményét.
Forrás: