A Foucault-inga fizikája
A következőkben nagyon röviden - szinte csak felsorolásszerűen - összefoglaljuk a Foucault-inga mozgásának megértéséhez szükséges legfontosabb fizikai tudnivalókat.
Vonatkoztatási rendszer
Bármely test (tömegpont) - például a Foucault-inga - helyzete, illetve annak megváltozása (mozgás) csak más testekhez viszonyítva értelmezhető. A mozgás tanulmányozása során tehát definiálnunk kell egy vonatkoztatási rendszert, amihez képest a vizsgált test pillanatnyi helyzetét megadjuk. A testek mozgásának leírásával a kinematika foglalkozik.
A vonatkoztatási rendszerhez képest rögzített helyzetű pontok, vonalak, felületek rendszere a koordináta-rendszer, ami a vizsgált testek vonatkoztatási rendszerhez viszonyított helyzetének számszerű jellemzésére szolgál. Ilyen például a térbeli derékszögű vagy Descartes-féle koordináta-rendszer, vagy a térbeli polárkoordináta-rendszer. A test vonatkoztatási rendszerhez képesti helyzetét a koordináta-rendszer kezdőpontjából (O) a pontszerűnek tekintett testhez (P) mutató r helyvektorral jellemezzük.
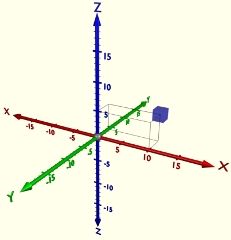
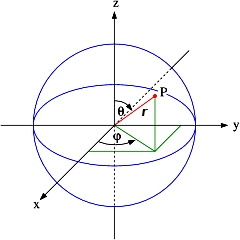
A térbeli Descartes-féle koordináta-rendszerben a test helyzetének jellemzésére az (x,y,z) koordinátákat, míg a térbeli polárkoordináta-rendszerben az (r,φ,θ) koordinátákat használjuk.
A tehetetlenség törvénye
A testek mozgásának tanulmányozásakor általában nem elégszünk meg annak megválaszolásával, hogy az más testekhez viszonyítva hogyan történik, hanem az okra is kíváncsiak vagyunk, azaz arra, hogy a vizsgált test mozgásában más testeknek mi a szerepe. Ezzel a kérdéssel a dinamika foglalkozik.
A Newton-féle első axióma, más néven a tehetetlenség törvénye kimondja, hogy minden test nyugalomban marad vagy egyenes vonalú egyenletes mozgást végez mindaddig, míg más testek hatásai ezen állapotának megváltoztatására nem kényszerítik. A testek azonban a mozgásállapot megváltoztatására irányuló hatásnak ellenszegülnek, ez a tulajdonság a tehetetlenség.
Az olyan vonatkoztatási rendszerek, melyekben érvényes az első axióma, az inerciarendszerek. Sok mechanikai jelenség leírása szempontjából a Földhöz rögzített vonatkoztatási rendszerek inerciarendszernek tekinthetők.
A dinamika alaptörvénye
Ha egy testnek egy inerciarendszerhez viszonyított v sebessége megváltozik, azt mindig más test(ek) hatásának tulajdonítjuk. Ez a hatás az erő. A gyorsulás azt mutatja meg, hogy milyen ütemben változik a sebesség:
a = dv/dt = d2r/dt2.
Amint már említettük, a testek ellenállnak a mozgásállapotuk (sebességük) megváltoztatására irányuló hatásnak. Az ellenállás mértékét jellemző, a test tehetetlenségét kifejező fizikai mennyiség a (tehetetlen) tömeg.
Azt, hogy a testre erő hat, a test sebességének megváltozásából, a gyorsulásából ismerjük fel: a = f(F).
Az előzőeket foglalja össze a Newton-féle második axióma, más néven a dinamika alaptörvénye:
F = ma,
azaz egy testre ható erők eredője egyenlő a test (tehetetlen) tömegének és gyorsulásának szorzatával. Természetesen az ok-okozati viszonyokat is figyelembe véve ezt inkább az
a = F/m
alakban kellene felírni.
A Galilei-féle relativitási elv
A Galilei-féle relativitási elv azt mondja ki, hogy az egymáshoz képest egyenesvonalú egyenletes mozgást végző vonatkoztatási rendszerek a mechanikai jelenségek leírása szempontjából teljesen egyenértékűek. A mellékelt ábra alapján könnyen kimutatható, hogy az egymáshoz képest egyenesvonalú egyenletes mozgást végző K és K' vonatkoztatási rendszerben a test gyorsulása ugyanaz:
d2r/dt2 = a = a' = d2r'/dt2.
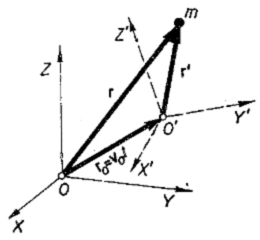
Az egymáshoz képest egyenesvonalú egyenletes mozgást végző K és K' vonatkoztatási rendszerben a test gyorsulása ugyanaz.
Mivel a testre ható erők csak a többi testhez viszonyított helyétől, sebességétől és az időtől függhetnek, az előbbiek alapján a K és K' vonatkoztatási rendszerben ugyanúgy néz ki a dinamika alapegyenlete, ez pedig azt jelenti, hogy a K és K' mechanikai jelenségek alapján nem különböztethető meg!
Jó példa lehet erre a vasútállomáson egymás mellett álló, de ellentétes irányú vonatok esete. Ha az egyik szerelvény - lassan - elindul, nem tudjuk megmondani, hogy a mi vonatunk indult-e el vagy a mellettünk álló. Biztosak csak akkor lehetünk a dolgunkban, ha az állomásépületet is látjuk. Vagy mégsem?
(A vasútállomásos példa jól mutatja, hogy mennyire a földhöz akarunk mindenfajta mozgást vonatkoztatni.)
A tehetetlenségi erő
Láttuk tehát, hogy egymáshoz képest egyenesvonalú egyenletes mozgást végző vonatkoztatási rendszerek egyenértékűek a mechanikai jelenségek leírása szempontjából. Egymáshoz képest gyorsuló vonatkoztatási rendszerekre azonban ez már nem igaz!
Képzeljük el a következő kísérletet. Egy kocsira szerelt asztal mellett egy megfigyelő ül, előtte az asztalon egy golyó van. A golyó és az asztal közötti súrlódás elhanyagolható. Legyen a K vonatkoztatási rendszerünk a teremhez rögzítve (és ezt tekintsük most inerciarendszernek), a K' pedig az asztalhoz. Az asztalt mozgassuk a0 gyorsulással az ábrán jelzett irányban egyenes vonalban. Hogyan értelmezi a K-ban és a K'-ben helyet foglaló megfigyelő a bekövetkező jelenséget?
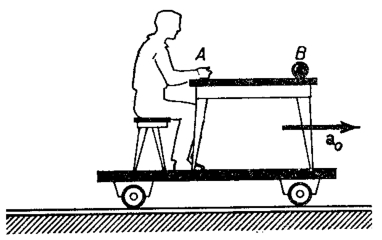
Inerciarendszerhez képest egyenesvonalú, de gyorsuló mozgást végző koordináta-rendszerben a dinamika alaptörvénye csak akkor lesz változatlan formában érvényes, ha a valódi erők mellett a gyorsulással ellentétes irányú ún. tehetetlenségi erőt is figyelembe vesszük.
A K-ban helyet foglaló megfigyelő azt fogja mondani, hogy a golyóra ható erők eredője zérus, ezért az nyugalomban van, a kocsin helyet foglaló ember közeledik a golyó felé. Ezzel szemben a K'-ben helyet foglaló megfigyelő szerint a golyó −a0 gyorsulással mozog felé, ő pedig ehhez igyekszik valami erőhatást párosítani.
Ha a dinamika alaptörvényét a K' rendszerben is érvényesnek akarjuk tekinteni, akkor azt kell mondanunk, hogy ebben a rendszerben, azaz az inerciarendszerhez a0 gyorsulással mozgó vonatkoztatási rendszerben az inerciarendszerben is fellépő erőkhöz még a nem valódi
Fteh = −ma0
tehetetlenségi erőt is hozzá kell adnunk.
A centrifugális erő
Legyen továbbra is a K rendszerünk az előadóteremhez rögzített inerciarendszer, a K' pedig a K-hoz képest állandó ω szögsebességgel forgó rendszer, például az ábrán látható asztallal kombinált forgó zsámoly. A zsámolyon helyet foglaló megfigyelő egy dinamométeren keresztül tartja r sugarú körpályán az m tömegű P golyót. Azt tapasztalja, hogy az erőmérő mω2r nagyságú erőt jelez.
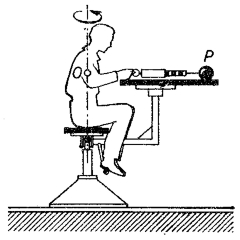
Forgó rendszerben az inerciarendszerben fellépő erők mellett egy sugárirányban kifele mutató tehetetlenségi erőt, a centrifugális erőt is figyelembe kell vennünk.
A K-ban nyugvó megfigyelő azt mondja, hogy a golyó egyenletes körmozgást végez az r sugarú körpályán, az ehhez szükséges Fcp = −mω2r centripetális erőt az erőmérő megnyúlt rugója fejti ki. Ezzel szemben a K'-ben nyugvó megfigyelő (a zsámolyon forgó személy) a golyót nyugalomban látja, de érzi az izmai által kifejtett −mω2r erőt, ezért az a következtetése, hogy a golyóra egy mrω2 nagyságú, de kifele mutató erőnek is kell hatnia. A forgó rendszerben elhelyezkedő megfigyelő által érzékelt kifele mutató erő a centrifugális erő:
Fcf = mω2r.
A Coriolis-erő
Tegyük fel, hogy a zsámolyon ülő megfigyelő az ábrának megfelelően a P pontban elengedi a bekormozott, s így a pályájának felrajzolására alkalmas golyót.
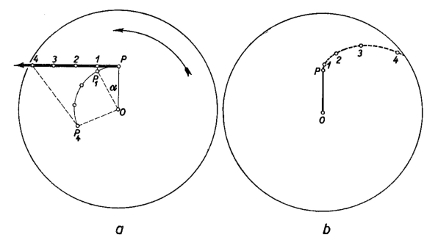
Forgó rendszerben a centrifugális erőn kívül egy másik tehetetlenségi erő is fellép, ami a testet a mozgásirányához képest oldalra téríti el.
A K-ban nyugvó megfigyelő azt mondja, hogy az elengedés után a golyóra már nem hat erő (a súrlódás elhanyagolható), így az a vP = rω érintő irányú sebességét megtartva fog mozogni a P-1-2-3-4- egyenes mentén (lásd az ábra (a) része). A K'-ben helyet foglaló megfigyelő ezzel szemben azt tapasztalja, hogy az elengedett golyó sugárirányban kifele indul el, amit ő a centrifugális erő hatásának tulajdonít. Gyorsan észreveszi azonban, hogy a golyó eltér oldalirányban, és a P-1-2-3-4- görbe mentén (lásd az ábra (b) része) mozog. Ebből viszont azt a következtetést vonja le, hogy a forgó rendszerben a centrifugális erőn kívül másik tehetetlenségi erő is hat. Ez a Coriolis-erő, melynek iránya merőleges a test sebességére és a forgástengelyre is:
FCor = 2m v × ω.
A Föld mint forgó vonatkoztatási rendszer
Eddig a Földet inerciarendszernek tekintettük, de bolygónk forog a tengelye körül a nagyon távoli galaxisok által definiált inerciarendszerhez képest. A forgás szögsebessége ω = 2π/86164 s = 7,29 · 10-5 s-1. Kérdés, hogy vannak-e olyan jelenségek, melyeket a forgó Földön nyugvó megfigyelő csak a tehetetlenségi erők bevezetésével tud értelmezni, közvetett módon igazolva azt, hogy egy forgó rendszerben van.
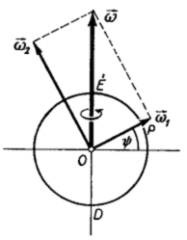
A Coriolis-erő hatását célszerű az ω vektor komponensei szerint tanulmányozni.
A centrifugális erő felelős a Föld lapultságáért, illetve a súly helytől való függéséért, ezekre a jelenségekre most bővebben nem térünk ki.
A Coriolis-erő hatásának vizsgálatához az ω-t bonstuk fel két komponensre: ω = ω1 + ω2. A ψ földrajzi szélességű P pontban ω1 merőleges a felszínre, ω2 pedig párhuzamos vele. Az ábra alapján
ω1 = ω sin ψ és ω2 = ω cos ψ,
a Coriolis-erő megfelelő komponensei pedig
FC1 = 2m v × ω1 és FC2 = 2m v × ω2.
A Coriolis-erő C2 komponensének hatásai
Az FC2 = 2m v × ω2 komponens egy függőlegesen eső testnél kelet felé mutató erőt jelent mindkét féltekén, így ez a komponens okozza például a szabadon eső testek kelet felé való eltérülését. Magyarországon 100 méter esési magasságnál ez az eltérés körülbelül 1,5 cm. Inerciarendszerből nézve az történik, hogy a Földdel együtt forgó test megtartja az elejtés előtt meglévő, kelet felé mutató, a talpponti sebességnél nagyobb sebességkomponensét is, ezért a talpponttól keletre fog földet érni.
Kelet-nyugati irányban mozgó test esetén az FC2 függőlegesen lefele mutat, így a nyugat (kelet) felé mozgó testek látszólagos súlynövekedést (súlycsökkenést) szenvednek. Ez az ún. Eötvös-effektus. Magyarországon egy 70 kg tömegű és 1 m/s sebességgel mozgó testnél értéke körülbelül 0,01 N.
A Coriolis-erő C1 komponensének hatásai
Az FC1 = 2m v × ω1 komponens az északi (déli) féltekén vízszintes síkban mozgó testnél a sebességre merőlegesen jobbra (balra) irányuló erőt jelent.
Ez a komponens felelős például
- a lövedékek jobbra (balra) történő eltéréséért az északi (déli) féltekén,
- az áramló levegő eltérítéséért, ezáltal az északkeleti és délkeleti passzátszelek kialakulásáért,
- a ciklonok keletkezéséért és a két féltekén eltérő forgásirányukért,
- valamint az inga lengési síkjának elfordulásáért!
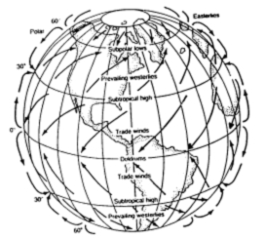
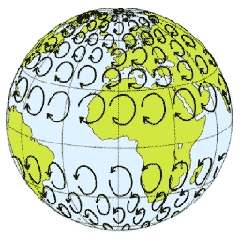
A Coriolis-erő felelős a földi légkör nagyléptékű mozgásainak, például a passzátszeleknek és a ciklonoknak egyes tulajdonságaiért, előbbiek esetében a mozgás, utóbbiak esetében a forgás irányáért.
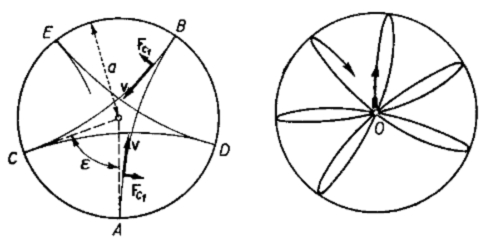
A Coriolis-erő okozza az inga lengési síkjának elfordulását is. Ha az ingát kitérített helyzetből indítjuk, a baloldalon látható nyomot rajzolja, ha pedig egyensúlyi helyzetből lökjük ki, akkor a jobboldali nyomot kapjuk.
A Foucault-féle ingakísérlet
A kísérletet először Jean Bernard Léon Foucault végezte el 1851-ben a párizsi Pantheon-ban egy 67 méter hosszú szálon függő 28 kg tömegű ingatesttel.
A ψ földrajzi szélességű helyen a lengési sík a Földhöz képest ω1 = ω sin ψ szögsebességgel forog, az északi féltekén észak-kelet-déli irányban:
ω1 = ω sin ψ ≈ 2π sin ψ nap-1 = 15° sin ψ óra-1.
Magyarországon ψ ≈ 47,5°, így sin ψ ≈ 0,74, azaz ω1 ≈ 5,4 · 10-5 s-1 ≈ 11° óra-1, tehát az inga lengési síkja óránként 11°-kal fordul el.
Egy 28,8 m hosszú, a = 2,5 m amplitúdójú, T ≈ 10,8 s lengésidejű inga esetében a lengési sík egy lengés alatti elfordulása ε = aTω sin ψ ≈ 1,3 mm. A lengési sík teljes körbefordulási ideje Magyarországon 24 óra/sin ψ ≈ 33 óra. A sarkokon a körbefordulási idő 24 óra, az egyenlítőn a hatás nem jelentkezik.
A Foucault-inga mozgását a vízszintes (x, y) síkban leíró differenciálegyenletek a következők:
d2x/dt2 − 2ω1dy/dt + Ω2x = 0,
d2y/dt2 + 2ω1dx/dt + Ω2y = 0,
ahol Ω2 = g/l, ahol g az adott helyen a gravitációs gyorsulás, l pedig az inga hossza.
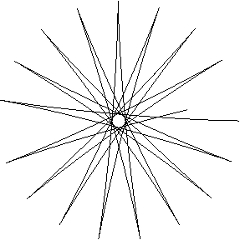
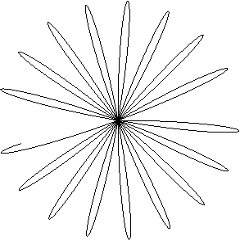
A Foucault-inga mozgásegyenleteit numerikusan integrálva felrajzoltathatjuk az ingatest által leírt pálya vízszintes síkra eső vetületét, az inga nyomát, amint a mozgás során a lengési síkja elfordul. A baloldali nyomot akkor kapjuk, ha az inga kitérített helyzetből indul, a jobboldalit pedig akkor, ha egyensúlyi helyzetében lökjük meg. Azért, hogy az egyébként lassú elfordulást érzékelhessük, az integrálás során a Föld szögsebességét a valódi hatszázszorosának választottuk. A kapcsolódó animációk itt és itt találhatók.
Ha az inga mozgását a távoli galaxisok által definiált inerciarendszerhez képest vizsgáljuk, akkor azt mondhatjuk, hogy az inga lengési síkja nem változik, a Föld fordul el alatta ω sin ψ szögsebességgel.